Method for energy gap calculation of large systems using quantum computers published in PNAS Tensor network-based phase difference estimation algorithm
Mitsubishi Chemical Corporation (Headquarters: Chiyoda-ku, Tokyo, President: Manabu Chikumoto, herein referred to as “Mitsubishi Chemical”), Keio University (Located: Minato-ku, Tokyo, President: Kohei Itoh), Softbank Corporation (Headquarters: Minato-ku, Tokyo, President: Junichi Miyakawa, herein referred to as Softbank), and JSR Corporation (Headquarters: Minato-ku, Tokyo, Tetsuro Hori as Representative Director, CEO, President Officer, "JSR") have developed a method for energy gap calculation of large systems using quantum computers. This work is the result of collaborative efforts within the IBM Quantum Network Hub, a part of the Keio University Quantum Computing Center※1. The resulting manuscript has been published in the Proceedings of the National Academy of Sciences (PNAS) and can be accessed at the following URL: Tensor-based quantum phase difference estimation for large-scale demonstration | PNAS.
Fundamental advancements
・Development of a tensor-based quantum phase difference estimation method, which combines energy gap calculation via quantum phase difference estimation with circuit compression via tensor networks
・Potential for high precision calculation of physical properties of large molecules
This work combines quantum phase difference estimation, a method for calculating the energy gap between states, and tensor networks, a framework for compression quantum circuits, to achieve high resolution of the energy gap of large molecules. This method was executed on IBM Japan’s commercially available gate-based quantum computers IBM Quantum System One and IBM Quantum System Two, where Hubbard models and linear molecule models were studied. By combining with an error suppression module in Q-CTRL, we successfully executed these systems up to 32 qubits, which are more than 5 times larger than previously studied systems.
This work is expected to pave the way for analysis of high-precision properties of large molecules.
Mitsubishi Chemical, Keio University, Softbank, and JSR will continue to explore quantum computing technology for a wide range of applications, including the development of materials.
※1:A cutting-edge quantum computer research center established by Keio University and IBM in May 2018 at Keio University's Faculty of Science and Technology. It is the first IBM Quantum Hub in Asia that enables cloud utilization of IBM's advanced quantum computers. Mitsubishi Chemical participates as a founding member in this industry-academia collaborative research center.
Background
All properties of a molecule can be understood by calculating the state of each of its electrons. However, the cost of this calculation increases exponentially with the number of electrons, so currently, approximations are used. For ground state calculations, the most widely used method is DFT, which approximates electron-electron correlations. However, DFT sometimes fails to achieve sufficient accuracy when applied to materials with complex electronic structures due to the strong Coulomb repulsion between electrons.
Quantum computers are a promising platform for making classically intractable calculations possible using quantum entanglement and superposition. The quantum phase estimation method is one of the most prominent algorithms in this area of research. It is thought that this algorithm can exponentially increase the speed of molecular energetic calculations; however, current quantum computers are noisy, and large quantum circuits are difficult to execute. At present, quantum phase estimation is limited to a maximum of 6 qubits.
Results of this study
In this work, we use quantum phase difference estimation and tensor networks to reduce the cost associated with quantum calculations. Quantum phase difference estimation uses the superposition of the ground and excited states to directly calculate the energy gap between the two. This energy gap is important in the calculation of physical properties. We choose quantum phase difference estimation over quantum phase estimation because the circuit for quantum phase difference estimation (Fig. 1a) lacks the ancilla-controlled gate on the time evolution operator, exp(-iHt), present in the circuit for quantum phase estimation (Fig. 1b). This decreases computational cost.
We then apply a framework called a tensor network to the resulting circuit, which further compresses it (Fig. 1c). This framework involves leveraging classical computers to search for shallow circuits that approximate a target circuit. An auxiliary benefit is that the implementation of the initial state preparation circuit suppresses noise exponentially.
Using this method, we execute a 32-qubit Hubbard model (Fig. 2a) and a 20-qubit decapentaene model on real quantum hardware. Here, our target physical property is the energy gap. We achieved further circuit compression by incorporating Q-CTRL’s error suppression module, reducing the number of controlled-Z gates required from 7,242 (with standard transpilation) to just 794 in the best case. As a result, we see a narrowing of the distribution of measurements to within 10 millihartrees of the reference value, confirming the successful execution of the algorithm. These results represent more than a 5-fold increase in system scale compared to previous studies using quantum phase estimation-type algorithms.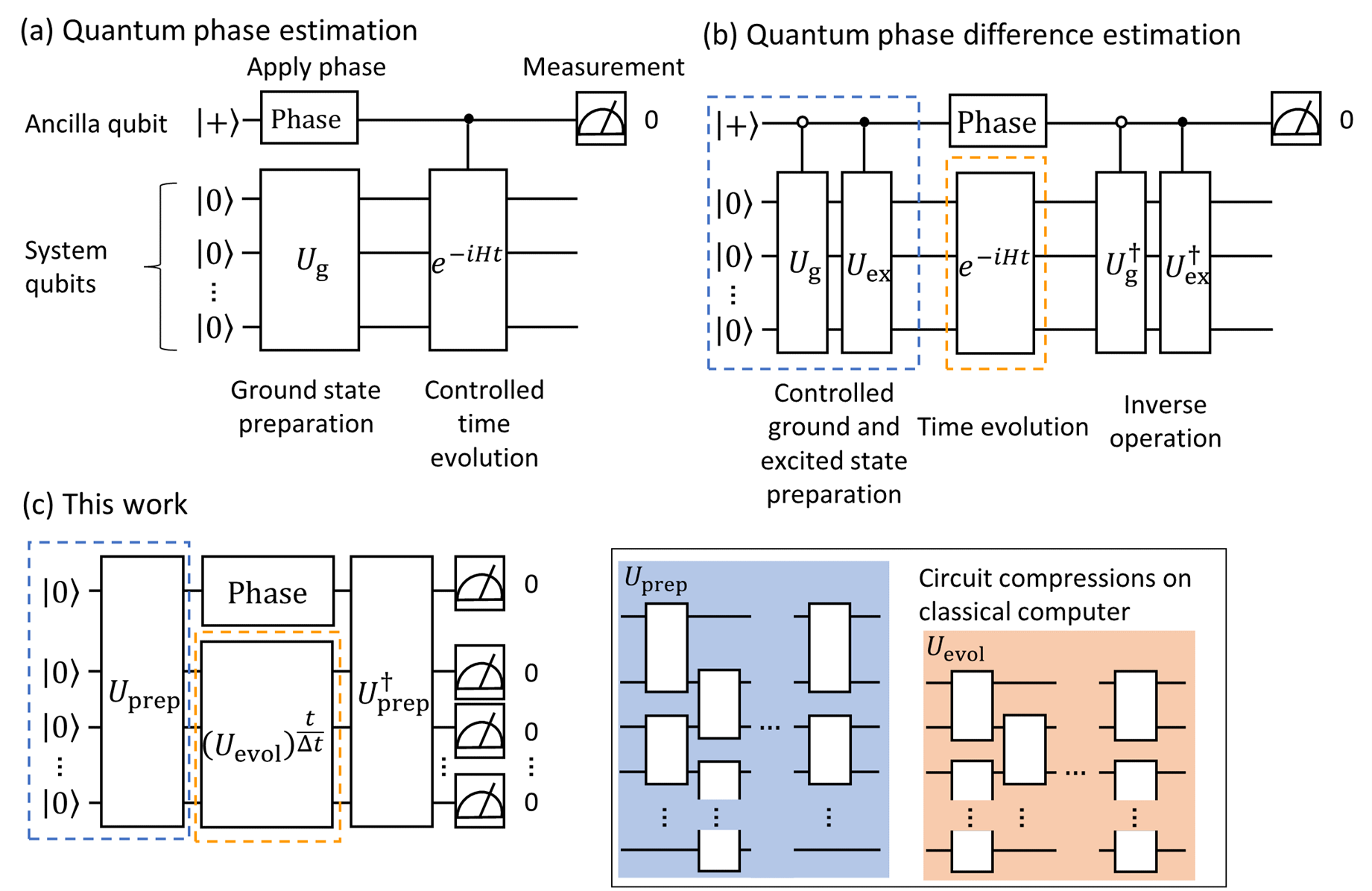
Figure 1. Overview of TQPDE
(a) Quantum phase estimation circuit (Bayesian type). The uppermost qubit is the ancilla qubit, and all others are system qubits. Ug prepares the approximate ground state, Phase imparts the phase, exp(-iHt) executes controlled time evolution, and finally, the ancilla qubit is measured. The probability of obtaining the outcome 0 when performing a measurement in the X basis has cosinusoidal dependence on the phase. When the phase aligns with that of the ground state energy, a peak appears in the distribution. The peak width can be adjusted by changing the length of the time evolution variable t, and by iterating this process, we refine the value of the energy gap.
(b) Quantum phase difference estimation circuit. The difference between two energy states is calculated, rather than the absolute energy of a single state. Ug and Uex prepare the required ground and excited energy states. These two controlled state preparation circuits replace the controlled time evolution in (1a), which decreases the computational cost. Generally, state preparation is simpler than time evolution.
(c) Proposed circuit. Tensor networks are used to generate shallower approximations of the circuits for state preparation and time evolution, Uprep and Uevol, respectively. Since short-term dynamics are efficiently calculated on classical computers, we first compress the short-term Δt dynamics calculation on a classical computer to create Uevol. Then, by repeating t/Δt times, we execute long-term dynamics on a quantum circuit. For measurement, we use the probability of obtaining 0 for all qubits when performed in the Z basis. This measurement exponentially suppresses noise.
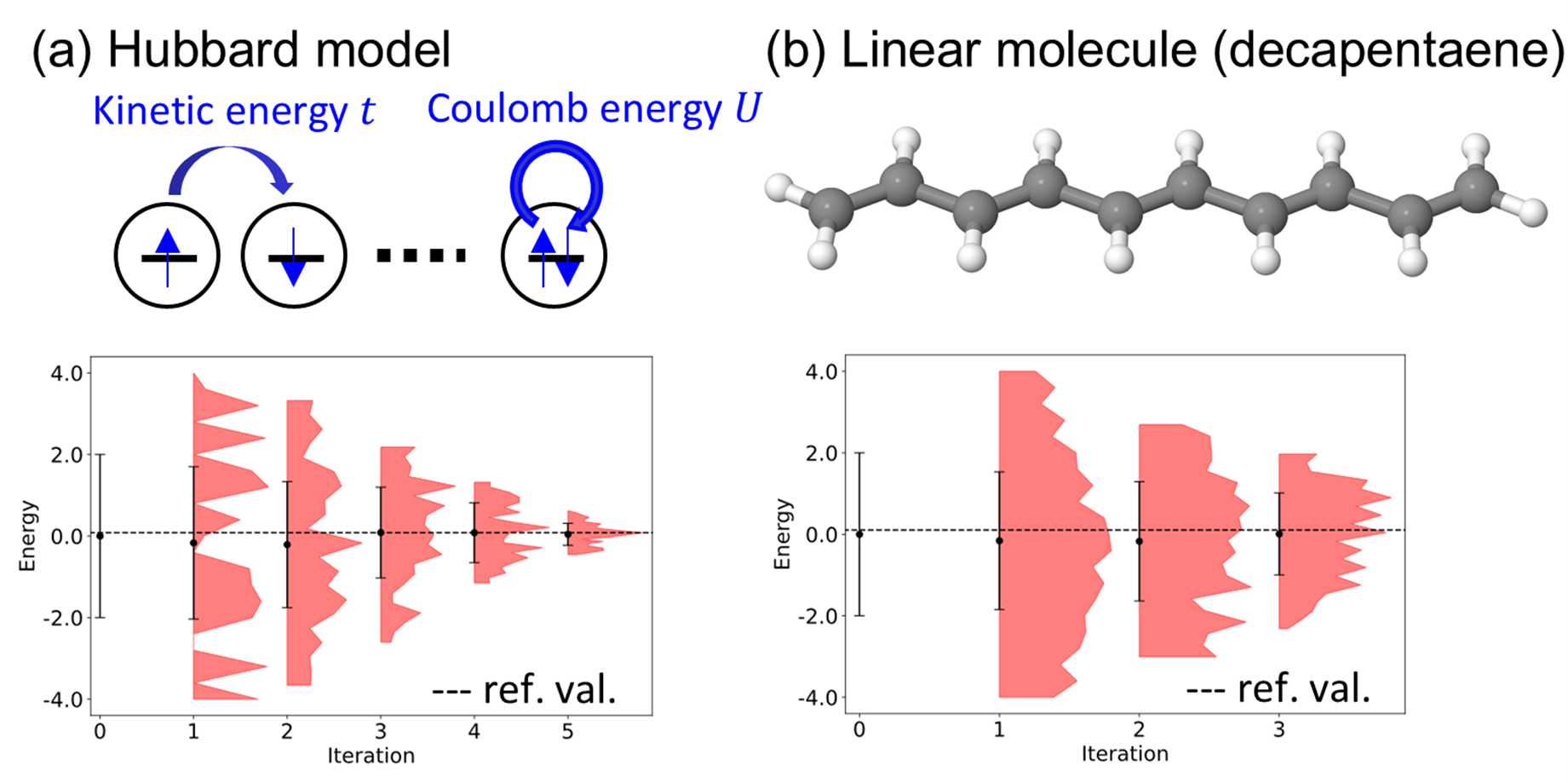
Figure 2. Calculation target and experimental results
(a) The Hubbard model. The Hubbard model is the simplest model that deals with electron-electron correlations. It consists of a kinetic energy term, t, and a Coulomb energy term U. Below are the calculation results for a 32-qubit system. The red distribution is the probability distribution from sampling the phase, and the peak corresponds to the value of the energy gap. As the number of iterations increases on the horizontal axis, the time evolution window increases and the distribution (in other words, the period of the cosine function) narrows. With each iteration, the distribution approaches the reference value for the energy gap (dashed line), demonstrating the effectiveness of our proposed method on real quantum hardware.
(b) The linear molecule model. The molecular model is more complex than the Hubbard model, but after performing orbital localization, we were able to perform calculations on 20 qubits.
Outlook
Quantum phase estimation is a hallmark of quantum algorithms, with a wide range of potential applications in prime factorization and machine learning, as well as chemistry. Previously, applications of quantum phase estimation have been limited to toy models small enough to verify on a classical computer. In this work, we perform calculations on systems approaching the limit of feasible calculation size on a classical computer. We believe that these results bring quantum computing closer to practical applications.
Glossary
Ground state: A state of electrons with the lowest energy
DFT: an acronym for density functional theory
Quantum entanglement: The property of a qubit to exist in multiple states simultaneously
Quantum superposition: The relationship where the states of multiple qubits are mutually dependent
Quantum circuit: A combination of quantum gates and measurements that control the quantum state of a qubit
Tensor network: A tensor is a data structure that generalizes scalars (0-dimensional), vectors (1-dimensional), and matrices (2-dimensional) to arbitrary dimensions. A tensor network is a graph structure that connects tensors. In our case, quantum gates are treated as tensors.
Excited state: A state of electrons with higher energy than the ground state configuration
List of coauthors
Mitsubishi Chemical Corporation: Shu Kanno, Takao Kobayashi, Qi Gao
Keio University: Kenji Sugisaki (at the time), Hajime Nakamura, Naoki Hamamoto
Softbank Corporation: Hiroshi Yamauchi
JSR Corporation: Rei Sakuma
Related press releases
・ A joint paper on “a new computational method for energy calculations of photonic materials on quantum computers” was published in a Nature Research Journal(February 9, 2023)
